Léon Foucault imagina le test qui porte son nom en 1858 pour contrôler la qualité des miroirs aluminés qu’il réalisait pour l’observatoire de Paris. Cette méthode est encore la méthode la plus utilisée par les astronomes amateurs qui fabriquent leur propre miroir. Ceci s’explique par le fait que fabriquer un banc de test met en œuvre quelques composants bon marché, et qu’elle peut se faire au rayon de courbure d’un miroir asphérique, typiquement parabolique, sans faire appel à un coûteux miroir plan d’autocollimation. De plus elle permet une bonne précision des mesures si elles sont réalisées par un opérateur aguerri.
Le principe du test de Foucault consiste à placer une source lumineuse au centre de courbure du miroir qui est testé. Si le miroir est parfaitement sphérique, la lumière revient sur son chemin après avoir été réfléchie par le miroir et refocalise sur la source.
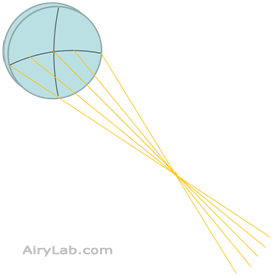
Note : Par simplification, nous ne considérons que quelques rayons sur un même plan et que la source est ponctuelle et virtuelle. En pratique la source est décalée de la position de l’observateur dans le plan parallèle au miroir. De même la source utilisée est une fente lumineuse, plus simple à réaliser qu’un petit trou régulier.
Si un observateur regarde le retour de la lumière au centre de courbure, il verra le miroir uniformément illuminé, celui-ci renvoyant la lumière de manière parfaitement homogène en un point.
Si nous déplaçons un obstacle – appelé couteau de Foucault – placé dans le plan du centre du rayon de courbure transversalement vers le point de focalisation, nous pouvons nous attendre à ce que celui-ci coupe la lumière qui revient du miroir au passage de l’axe optique.
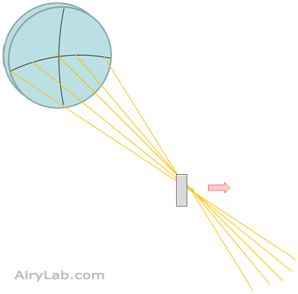
En pratique, et à cause de la diffraction, la lumière va disparaître progressivement à mesure que le couteau progresse. Néanmoins la lumière réfléchie par le miroir reste homogène et l’observateur qui regarde derrière le couteau verra un assombrissement progressif de celui-ci. L’intensité lumineuse restera homogène ; c’est la « teinte plate ». Lorsque le couteau aura suffisamment progressé, la lumière sera coupée simultanément en tout point de l’image du miroir. La raison étant que le miroir étant sphérique, toute la lumière revient en un point.
Si l’on avance ou recule le couteau le long de l’axe optique, déplacer le couteau latéralement ne coupera plus tous les rayons simultanément mais progressivement.
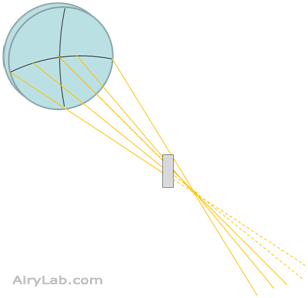
Lorsque le couteau aura atteint l’axe optique, le miroir apparaîtra à moitié éteint.
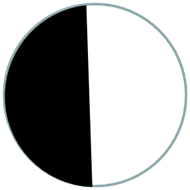
Selon que le couteau est avant ou après le centre de courbure, la partie illuminée sera l’une ou l’autre moitié. En effet l’image s’inverse après avoir convergé au centre de courbure.
Dans le cas plus fréquent du miroir parabolique qui équipe les télescopes, les rayons ne convergent pas tous en un seul point au rayon de courbure, mais sur une plage plus étendue à cause de l’aberration de sphéricité induite par le fait qu’on ne travaille pas en conjugaison infini-foyer.
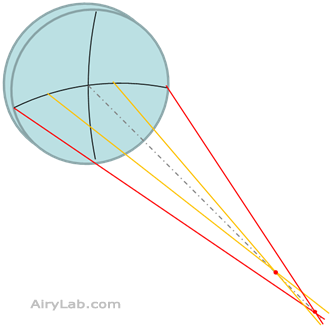
Si l’on représente seulement trois paires de rayons A,B et C issus de différentes zones du miroir en deux dimensions, nous avons trois foyers différents pour ces trois paires de rayons. Il s’agît bien évidemment d’une simplification.
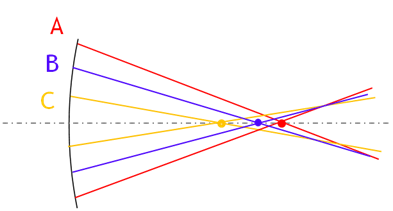
Regardons maintenant ce qu’il se passe lorsque nous introduisons le couteau de Foucault.
– Dans un premier temps, le couteau vient couper les rayons réfléchis par le miroir au niveau du point de focalisation des rayons C. Pour ceux-ci, nous aurons une teinte plate car nous sommes au point de focalisation. En revanche les rayons B et A seront coupés en amont de leur focalisation et nous aurons donc une moitié qui sera éclairée, et l’autre qui sera obscurcie.
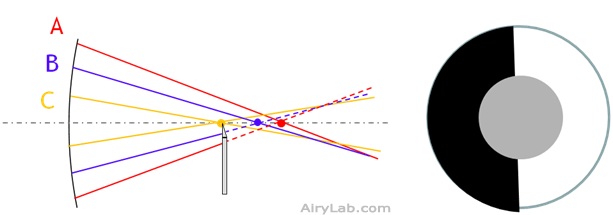
– Maintenant amenons le couteau du niveau du point de focalisation des rayons B. Pour cette zone du miroir, nous aurons une teinte plate. Pour les rayons A il n’y a pas de changement. En revanche les rayons C seront à moitié arrêtés eux aussi, mais après leur point de focalisation. Donc les zones éclairées et obscurcies des rayons A et C seront inversés.
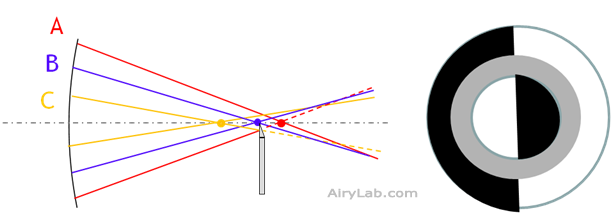
– Amenons enfin le couteau au niveau du point de focalisation des rayons A. La partie extérieure prendra à son tour une teinte plate. En revanche les rayons B et C seront coupés à moitié en aval de leur point de focalisation.
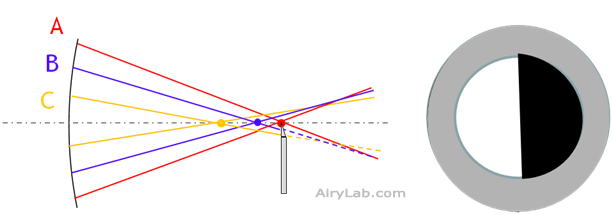
En connaissant les caractéristiques du miroir (diamètre et focale), il est possible de connaître les points de focalisation des rayons en fonction de leur distance par rapport à l’axe optique du miroir. Il s’agît d’un calcul lié à l’aberration sphérique due à la conjugaison au centre du rayon de courbure. Il est donc possible de vérifier la conformité du miroir à la forme théorique en vérifiant que l’on obtient bien la teinte plate pour une position des rayons au point de focalisation théorique sur l’axe optique.
Pour cela, on place devant le miroir un masque appelé masque de Couder qui délimite des zones concentriques pour chacune desquelles l’appareil de Foucault va permettre de déterminer la position de focalisation.
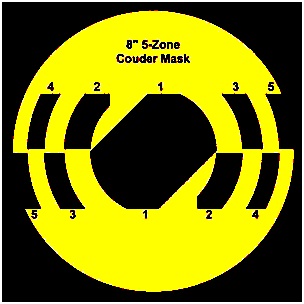
Les zones noires sont découpées dans du carton, et la partie jaune restante est placée devant le miroir. Ensuite, pour chacune des zones de 1 à 5, on relève la position de l’appareil de Foucault qui a permis d’obtenir une teinte plate (quand des deux fenêtres d’une même position sont illuminées) et qui correspond à chacun des points de focalisation.
Ainsi obtient on les écarts du miroir par rapport à la forme recherchée en autant de points que le masque de Couder comprend de zones de mesure. Il est possible de pivoter le miroir pour obtenir des mesures sur plusieurs axes.
L’appareil de Foucault en lui-même se compose d’une source lumineuse, en général une fente et d’un couteau. L’ensemble est fixé sur un chariot en translation le long de l’axe optique et sur lequel on peut relever la position à quelques dizaines de microns près. Le couteau est également mobile transversalement à l’axe optique pour venir couper le faisceau de retour.
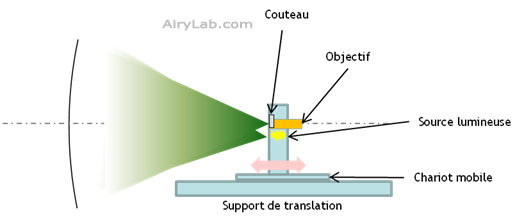
Il est possible d’asservir les déplacements et les mesures avec un ordinateur et un système de moteur pas à pas pour des mesures plus précises et reproductibles et également une meilleure résolution spatiale.
Le Foucault est un test qui donne également des informations qualitatives quand à la qualité de la surface du miroir puisque des écarts très faibles sur le verre sont mis en évidence par les changements de teinte dus au décalage du point de focalisation. Même si les défauts mis en évidence ne sont pas aussi petits que pour un test de Lyot, cela permet de détecter des mamelonnages locaux et des défauts de zone.
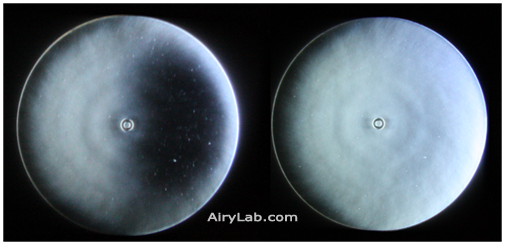
Voici par exemple un Foucault d’un miroir censé être parabolique. Sur l’image de droite, on note qu’on arrive à obtenir une teinte plate sur presque l’ensemble du miroir, ce qui montre une parabolisation très insuffisante. De même on peut relever des traces d’usinage et un état de surface médiocre.
Avantages du Foucault
– Fabrication simple et peu couteuse
– bonne précision avec un utilisateur expérimenté
– permet un contrôle qualitatif visuel des défauts de surface du miroir, permet la prise de vue
– robustesse du test en recoupant la perception visuel du miroir avec les données chiffrées relevées
– permet le contrôle de surfaces asphériques
– peut être pratiqué sur une lunette également avec un miroir plan, et sur un miroir non aluminé.
Inconvénients
– Demande une bonne maîtrise et une bonne compréhension du processus
– requiert une bonne précision des mesures du déplacement du chariot
– permet de mesurer seulement les défauts de révolution
– la résolution spatiale est très faible : seulement quelques points de mesure par axe
– temps de mise en œuvre important
