Les aberrations optiques déforment le front d’onde sphérique qui converge au point focal d’un instrument. La conséquence de cette déformation est que la focale de l’instrument varie localement. Une autre conséquence est un décalage de la phase par rapport à la phase attendue. La modélisation en polynôme de Zernike par exemple est une expression de la modification de la phase. Les opticiens lorsqu’ils désignent les défauts d’un système optique disent que l’onde est en retard ou en avance de quelques nanomètres, ou de L/x, x étant une fraction de la longueur d’onde. Le retard ou l’avance de l’onde est le retard ou l’avance de sa phase. Caractériser une optique est donc, en résumé, chercher à obtenir une carte de phase.
Une voie différente de l’interféromètre serait d’obtenir directement la carte de phase sur le capteur d’une caméra. La difficulté à obtenir directement cette carte de phase tient au fait que les capteurs CCD ne sont sensibles qu’aux variations d’intensité de la lumière et ne détectent pas les variations de la phase.
En 1985, M.Teague a mis en équation l’intensité lors de la propagation d’une onde en fonction de la distribution de la phase et de l’intensité initiales. C’est l’équation de transfert en intensité. Cette équation montre que les écarts en intensité du front d’onde dépendent de l’intensité initiale au début de la propagation ET des écarts de la phase initiale. De plus ces écarts d’intensité s’accentuent lors de la propagation de l’onde.
En un point z de la propagation l’intensité de l’onde dépend de l’intensité de l’onde au point d’origine selon l’équation suivante :

Où Iz et I0 sont les intensités au point 0 d’origine et au point Z de la propagation et ϕ0 est la phase à l’origine. Il est donc possible de retrouver la phase à l’origine en fonction des variations d’intensité.
Si l’intensité à l’origine est constante, et que donc le terme I0 est connu et constant sur l’ensemble du front d’onde, on peut résumer graphiquement cette équation comme suit :
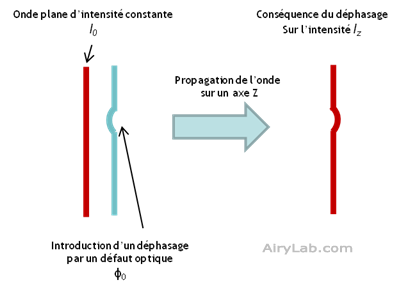
Plus la propagation de l’onde est importante et plus les écarts d’intensité le seront aussi. Cela peut se faire par une réduction de la pupille à travers un afocal (représentation simplifiée) :

Néanmoins ceci se fait au détriment de la résolution spatiale. Ce principe s’applique pour tous les systèmes d’analyse du front d’onde par l’équation de transfert en intensité : il y a un compromis entre la sensibilité (plus petit défaut mesurable) et la résolution spatiale (nombre de mesure par unité de surface).
Ce phénomène – un décalage de phase qui donne une variation d’intensité – est connu empiriquement depuis des millénaires par exemple pour la confection des miroirs magiques Chinois. C’est également ce qui permet de voir l’ombre projetée par la turbulence de l’air.

Un miroir en apparence parfaitement plan va donner un motif de variation d’intensité dans l’image qu’il réfléchit. En réalité le miroir n’est pas plan mais légèrement martelé. Ces très légères différences de niveau sur la surface du miroir vont provoquer un déphasage de l’onde réfléchie qui se traduira après propagation en variation d’intensités. Il est donc possible de détecter des écarts de quelques dizaines de nanomètre avec nos simples yeux.
Une autre façon de visualiser ce phénomène est possible en optique géométrique. Comme nous l’avons vu, le déphasage de l’onde qui traverse un objectif transmissif va modifier ponctuellement la distance focale de celui-ci. Si l’on intercepte une onde issue d’une étoile en amont et en arrière du point de focalisation (PSF intra et extrafocale), ces déphasages vont modifier l’aspect des tâches d’Airy défocalisées qui aurait du être identiques si le front d’onde issu de l’instrument avait été parfait.
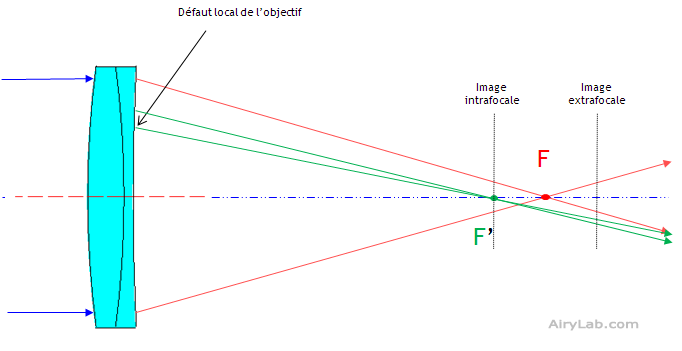
Il est donc possible de déduire de la comparaison des images intra et extra focales la carte de phase du front d’onde issue de l’objectif.
Cette méthode, appelée senseur de courbure, est utilisée pour la reconstruction de la carte de phase notamment dans des boucles d’optiques adaptatives sur des télescopes.
Comme nous l’avons vu au dessus, la position de défocalisation joue sur la sensibilité et sur la résolution spatiale. Plus on est loin du point focal et plus la résolution est importante au détriment de la sensibilité, et vice versa.
En métrologie cette méthode est plus difficile à mettre en œuvre car très sensible aux variations d’intensité qui peuvent ne pas être toutes dues à un déphasage mais d’autres causes comme des poussières sur la chaîne optique et de la turbulence sur le banc de mesure.
Avantages du senseur de courbure
– Analyse rapide
– résolution et sensibilité réglables
– adapté à des processus en temps réel
– pas d’optique de référence contrairement à l’interférométrie
Inconvénients
– Très sensible aux variations d’intensité et aux turbulences
– nécessite un alignement parfait des images intra et extra-focale au risque de générer des artefacts très importants
– nécessite une mécanique capable de produire deux images de défocalisation identiques (platine piézo ou membrane contrôlée)
– nécessite un front d’onde incident parfait de la taille de la pupille à mesurer, ou bien un système d’autocollimation.
