La réfraction ne concerne que les optiques astronomiques qui travaillent en transmission de la lumière et non pas en réflexion. Ce sont donc les lunettes, mais aussi les télescopes qui utilisent des correcteurs (la lame de Schmidt d’un Schmidt Cassegrain, un Newton avec un correcteur de coma ou le miroir Mangin d’un Klevtsov) ou des ménisques (Maksutov).
Le phénomène de réfraction, qui comme nous allons le voir permet de dévier la trajectoire des rayons lumineux, est le principe de base de la conception des objectifs des lunettes en permettant de faire converger des rayons lumineux parallèles sur l’axe optique au foyer F de l’instrument, et donc de pouvoir créer une image. Les lentilles peuvent bien sûr fonctionner dans d’autres combinaisons que celle de l’infini-foyer.
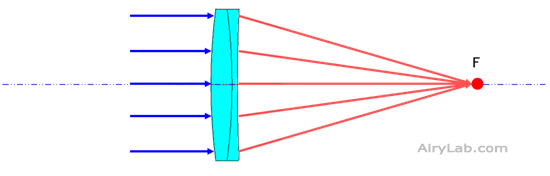
Si l’on considère ce phénomène en terme de front d’ondes, la réfraction d’un objectif permet de transformer un front d’onde plan émis par une étoile en front d’onde sphérique qui converge au foyer en une image ponctuel de l’étoile sur l’axe optique.
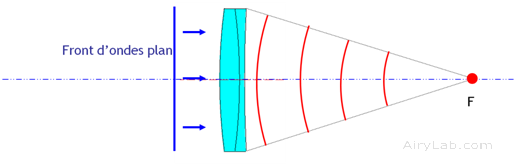
Dans le cas d’une autre combinaison, la lentille va modifier le rayon de courbure du front d’onde.
Pour modéliser la réfraction, il faut nous intéresser à la vitesse de la lumière.
Comme nous l’avons mentionné précédemment, la vitesse de la lumière est certes invariante dans le vide, mais elle varie selon son milieu de transmission. Elle se transmet par exemple moins vite dans le verre. La vitesse de la lumière est d’ailleurs une caractéristique importante des matières transparentes et est quantifiée par un indice, appelé indice de réfraction, et noté n.
Cet indice est calculé en référence à la vitesse de la lumière c dans le vide en prenant en compte la vitesse de la lumière dans le milieu transparent :
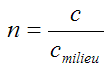
Pour le vide, indice de référence, n est par définition égal à 1. Pendant longtemps, la valeur 1 a été par convention la valeur de l’indice de réfraction de l’air. Il s’avère en réalité que l’indice de l’air est légèrement supérieur de 0,02% à l’indice du vide. Cette différence reste négligeable. En revanche, l’indice de l’air varie aussi avec la température et l’atmosphère terrestre présente donc un gradient d’indice de réfraction qui a une influence tout à fait significative sur la lumière des objets qui nous intéressent en astronomie en la déviant , et ce d’autant plus que l’objet est bas sur l’horizon et donc que sa lumière traverse plus d’air et que le gradient est plus important.
Lorsque la lumière change de milieu, et donc de vitesse, elle va être déviée selon la seconde loi de Snell Descarte. Si l’on considère la surface qui limite chacun des milieux d’indice différent et que l’on appelle un dioptre, le changement de direction se calcule en fonction des indices de chaque milieu et de l’angle d’incidence de la lumière par rapport à la normale du dioptre.
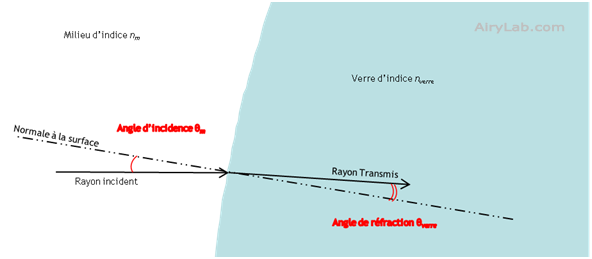
La relation entre les indices et les angles est :
nm sinθm = nverre sinθverre
Il faut noter que dans le cas d’angles à incidence faible comme dans le cas de lentilles minces et de rayons parallèles à l’axe optique d’un front d’onde plan, il est possible de simplifier cette relation avec l’approximation de Gauss. Dans ce cas, la formule devient :
nm θm = nverre θverre
Cette approximation simplifie considérablement les calculs même si les logiciels de ray tracing permettent maintenant de s’affranchir de cette contrainte. En revanche, elle n’est applicable que sur des instruments qui ont un rapport focal (distance du foyer au centre optique) sur diamètre élevé : au moins 15 pour de petits diamètres. Dans ce cas, ces instruments sont dans les conditions de Gauss. Cette approximation n’est aussi possible que si les indices des deux milieux ne sont pas trop différents et si le diamètre de l’instrument n’est pas trop important.
En pratique les objectifs des réfracteurs modernes ont des rapports F/D inférieurs à 15 par l’utilisation de verres à indice de réfraction élevé et des diamètres parfois importants, et l’approximation de Gauss ne sera pas utilisée pour la métrologie et la conception de ces instruments. En revanche, les conditions de Gauss peuvent potentiellement s’appliquer à des dispositifs qui ont des courbures beaucoup plus faibles, comme par exemple les lames de Schmidt ou des correcteurs de champ.
Si l’angle d’incidence devient trop important, il n’y a plus transmission, mais réflexion des rayons lumineux. Même à des angles faibles, il y a des réflexions marginales dû aux défauts de rugosité de surface du verre qui peuvent induire des baisses de contraste : aussi les optiques ont maintenant des traitements spécifiques antireflets.
Pour le verre qui compose les objectifs de nos lunettes, différentes formules permettent d’obtenir des verres d’indices très différents. Voici par exemple quelques verres du catalogue du fabriquant Schott :
|
Verre |
Indice |
Application |
| BaK 4 |
1,56883 |
Prisme de jumelles |
| BaK 7 |
1,51680 |
Prismes, lames de correcteurs |
| FK51 |
1,48656 |
Verre Crown d’objectif à faible dispersion |
| LITHOTEC-CAF2 |
1,43385 |
Fluorine de synthèse pour objectif Apo |
| SF5 |
1,65412 |
Verre Flint d’objectif à haut indice |
On peut donc voir que la capacité qu’à une lentille à faire converger plus ou moins rapidement des rayons incidents parallèles va dépendre à la fois de la courbure de la lentille, et de l’indice de son verre. Cependant il faut savoir également que l’indice de réfraction des verres varie aussi selon la longueur d’onde du flux lumineux, et que malheureusement plus l’indice de réfraction d’un verre est élevé et plus cet indice varie selon la longueur d’onde (cf Chromatisme).
